本文作者：Albert_JIAO

2012 年 NBA 全明星周末刚刚举行不久，在巨星们各种秀技能的时候，死理性派冒充了一把技术指导，在战术板上列了一大推公式和数据，向那些久经赛场但“不懂科学”的队员们解释，关键时刻这球该怎么打。怎样做出有技术含量的指导？当然是靠高端的数学模型。

数学计算决定犯不犯规

让我们穿越回 2010 年 NBA 的一场比赛，火箭队对阵公牛队。在比赛还剩 10 秒结束的时候，火箭队领先 3 分，此时球权在公牛队手中。火箭队虽然离胜利只有一步之遥， 但公牛队还并没有放弃，他们希望在最后一次进攻中扳平比分，把比赛拖入加时。面对这最后一攻，火箭队其实有两个策略可供选择：一是尽力防守阻止公牛队投三分；二是主动犯规，不让公牛队有投三分的机会。如果当时你是火箭队的技术指导员，你会建议主教练选择哪个？

这其实是一道数学题，不妨让我们来算一算。

根据 NBA 的数据，2010 整个赛季三分球平均命中率是 35.5%，不过在离比赛结束还有 10 秒或更短、进攻方落后 3 分的特定情况下，面对严防死守和巨大压力，命中率就要打折扣了，只有大约 20%。火箭队如果主动犯规让进攻方罚球两次，会怎么样？公牛队若想扳平比分，在火箭队犯规后可以选择：罚进第一球罚失第二球，同时还要抢到进攻篮板，之后再把球投进，完成一次“1+2”。

一般情况下，罚进第一球的概率是 75.6%，任务并不算难。故意投失第二个罚球，应该属于 100% 可以完成的任务。但是第二个罚球不进，公牛队抢下进攻篮板的概率就比较小了，根据 NBA 的统计数据，只有 13.9%。到此为止，如果三件事情都发生，概率是 75.6% × 100% × 13.9% = 10.5%。另一方面，NBA 两分球得分率大约是 50%，也就是说在抢到进攻篮板后，公牛队最后能够进入加时赛的可能性也就是 10.5% 的一半，5% 左右。

按照以上的计算来看，两种策略比较起来，选择主动犯规，火箭队有 95% 的获胜希望；不犯规防 3 分，火箭队只有 80% 的获胜希望。还是犯规策略更胜一筹。现实情况是，主教练阿德尔曼采取了与上面计算得出的结论相反的策略，也就是不犯规，所有队员都踩在三分线上防守。结果公牛队的当家球星德里克?罗斯用一道美丽弧线绝杀了火箭队。双方只好打加时赛，火箭队最终输掉比赛。

当然，计算结果并不能代替主教练（否则球队老板雇个数学家就好了，那可比主教练便宜得多）。因为这个模型还很简单和理想化，忽略了很多影响因素。比如公牛队不同球员之间的三分球、罚球命中率相差很大，一个平均值意义有限；另外模型也只考虑了一个进攻回合的情况，实际上双方可能会反复互相犯规，导致局势更复杂；除此之外失误情况我们也没有考虑。虽然如此，这个结果依然有一定的参考价值。如果概率模型足够复杂和完备，准确率和可靠度超过“技术指导”，也并非一件不可能的事情。

24秒何时出手才最好

除了教球员们怎么防守，技术流的指导当然还会教球员们怎么进攻。美国物理学教授布莱恩?斯金纳（Brian Skinner）就曾做过研究，计算出了每轮进攻什么时候出手最好。我们知道按照比赛规则，每个回合有24秒的进攻时间，选择什么时机出手，可是影响成功得分的关键因素。

布莱恩把“何时出手”看做和著名的 37% 法则（ 参看 死理性派恋爱法：拒绝掉前面37%的人 ）看成同一类题目。在球场上 24 秒钟中某一时刻，如果遇到一个投篮机会，球员会考虑是直接投还是传给队友继续寻求更好的机会。

不妨把每一次投篮机会的好坏都用一个“机会值”表示，假设这个值最差（f1）到最好（f2）是均匀分布、随机出现的。另外布莱恩在模型里还假定，在 24 秒中的某一时刻如果球队遇到一个得分机会，要看这次机会值是否高于一个临界值，只有高于临界值时才值得一试。临界值跟剩下的时间成正比， 24 秒剩下的时间越少，对投篮机会的要求就要越低，例如 24 秒钟声即将临近，进攻队员别无选择，即使此时被对方五人围成一团，投篮机会很差（f1），也只好一试。此时的临界值很低。相反，如果 24 秒进攻时间刚刚开始，机会不好的话还可以先组织一下，等待更好的得分机会，比如发现对方篮下出现空挡时（f2）。 24 秒刚开始时的临界值会比较高。

除此之外，临界值也跟在剩下的时间能有多少次投篮机会，以及失误出现的概率有关（控球的时间越多，出现失误的概率就越大）。根据 NBA 的统计数据，布莱恩教授的模型假定投篮机会是随机产生的，平均 2.8 秒会有一次；失误也是随 机产生的，平均 100 秒会有一次。据此他为 24 秒中的每一个时刻计算出了相应的临界值。

当然真实比赛中，对于一次投篮机会，很难判断什么样的投篮“机会值”是 2，什么样的“机会值”是 1，不过一定符合有好有坏的分布。布莱恩虽然没办法说明具体就一个投篮机会而言是投还是不投，但我们可以根据这个模型和 NBA 的统计数据估算出平均情况下，在 24 秒的各个时刻，最佳的出手比例分配应该是多少。比如计算结果认为在最佳方案中，有 12% 的投篮在 9 到 10 秒的时间段内发生。球队尽量按照图里这条黑色曲线的比例分配 24 秒里各个时间段的出手比例，可以以获取最大的得分率。

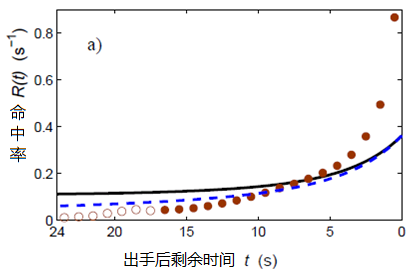
从上图可以看到，现实中 NBA 球队的平均出手时间相比于最佳曲线普遍稍晚一些（深红色点），如果改按照计算出的最佳时间分配出手，计算表明，球队每场比赛可以平均多得 4.5 分。果真如此的话，很多经常以小比分输掉比赛的球队就可以有机会反败为胜了。

手会热的发烫吗？

不少常看NBA比赛的球迷会有这样的感觉，某一球员可能在比赛的一段时间内突然爆发，接连命中十个八个，越投越来劲，怎么投怎么有。孙指导，张指导常常会把这种情况解释为“手热得发烫”。当然与之相反，球员也有“手冷”的时候，越投越投不中。一个球员接连投中几次之后，手真的会“变热”，再次投篮的命中率上升吗？理性的研究与直观的“赶脚”却是相反的。

首先任何人都承认，不管姚明，科比还是林书豪，比赛中都有那么几分钟超常发挥、高于平均命中率的时候，也一定有几分钟失常发挥的局面，只是这种超常失常的原因主要是因为巧合，还是真的因为命中之后让他们的手变热造成的？

拿扔硬币来说，虽然理论上正反两面的概率都是50%，但实际上连续扔很多次，也会遇到好几次总是正面，好几次总是反面的情况，可是硬币不会“热得发烫”，这只是统计上正常的波动。

早在二十多年前，美国康乃尔大学和斯坦福大学的三位研究者收集了当时费城76人队的比赛数据，对“手变热”一探究竟，看一看NBA比赛中连续投中、连续失手的情况是否和扔硬币一样，只是正常统计波动造成的错觉。

他们首先统计了费城76人队很多场比赛中，九名主力队员在连续投失三个球，两个球，一个球以及连续投进三个球、两个球、一个球六种情况下再次投篮分别的命中率，结果发现各名球员在六种情况下的命中率是基本相同的，甚至大多数球员在投失之后的命中率反而略高于投中之后的命中率。在统计上，只有这六种情况下存在差异，而且差异达到一定程度，才能断定“手热”，“手冷”存在，所以他们得出的结论只能是“无证据表明之前几次投篮结果与下一次投篮结果有关”。

接着，他们又把每位球员比赛中所有的投篮结果列成一列数据1110011010100100101……（1表示投中，0表示没有投中），连续的一个或者几个1看作一个“小段子”（像最前面的111）。如果手热现象存在，这些“小段子”的平均长度，也就是每次连投连中的平均个数会高于随机情况下的预期值。他们的结论是“没有异常”，也就是说这段数据更像是随机分布。

他们还用了一招，把上面的数据每相邻4个数字分为一组，看一下四投零中，四投一中，四投二中，三中，四中的情况的比例分布是否与随机情况的期望值有所不同，结果仍然是“完全正常”。

当然，有人会觉着一位球员连续投中之后，对方球员会加强对他的防守，他“手热”可能真的存在，但是表现不出来。研究者也研究了不存在对方球员干扰问题的罚球情形，发现第一个罚球投进以后，对于第二个罚球是否投进没有关联。他们还找了大学生球队的队员，在没有防守的情况下，让他们做不断变换位置投篮的试验，并且要求球员和旁观者估计什么时候“手热”，什么时候“手冷”，结果发现他们的数据仍然符合以上的结论，而且预测的正确率也就是半对半错，再一次说明“手热”并不存在。

根据他们的研究，前后投篮命中率之间的关联性是“怎么统计，怎么没有”，“怎么投怎么进”的情况更接近于扔硬币的自然波动，“手变热”、“手变冷”情况从理性角度完全看不到踪影。

参考资料

[1] Late-Game Defensive Strategy with a 3-Point Lead
[2]
[3] The problem of shot selection in basketball, Brian Skinner